Question 1: 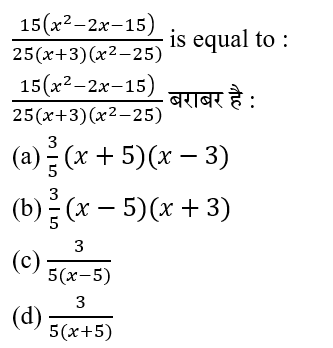
Question 2:
How many edges does a polyhedron with 8 faces and 12 vertices have ?
8 फलकों और 12 शीर्षों वाले किसी बहुफलकी के कितने किनारे होते हैं ?
Question 3:
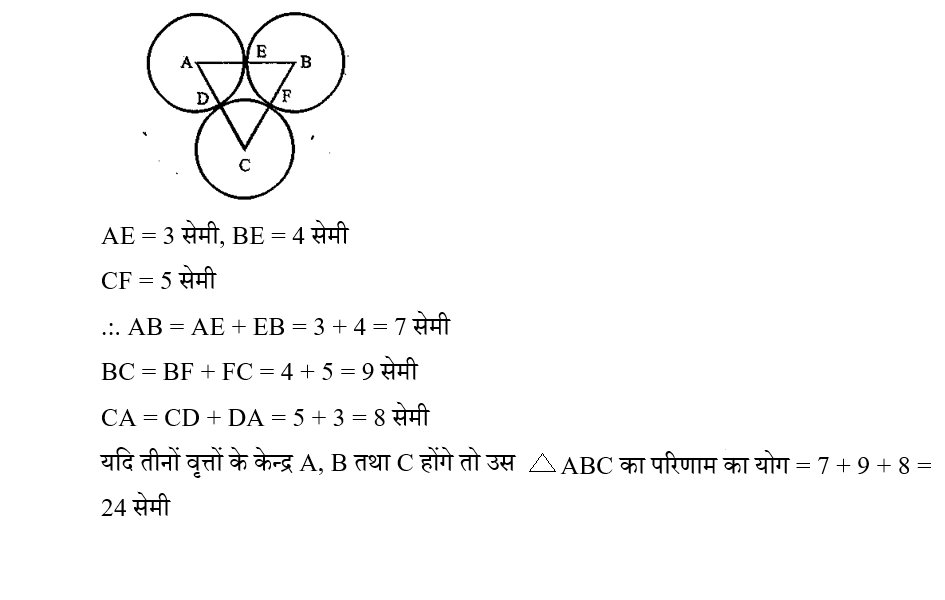
Three circles touch each other externally. Their radii are 3 cm, 4 cm and 5 cm. If the centers of those circles are A, B and C, then find the perimeter of ∆ABC.
तीन वृत्त एक दूसरे को बाह्यतः स्पर्श करते है। इनकी त्रिज्याएँ 3 सेमी, 4 सेमी एवं 5 सेमी है । यदि उन वृत्तों के केन्द्र A, B एवं C हों, तो ∆ABC का परिमाप ज्ञात कीजिए ।
Question 4:
A bag contains 6 red and 4 blue balls. What is the probability that a ball drawn at random from this bag will be red?
एक थैले में 6 लाल एवं 4 नीली गेंदें है क्या प्रायिकता है कि इस थैले में से एक गेंद यदृच्छया निकालने पर वह लाल रंग की होगी?
Question 5: 
Question 6: 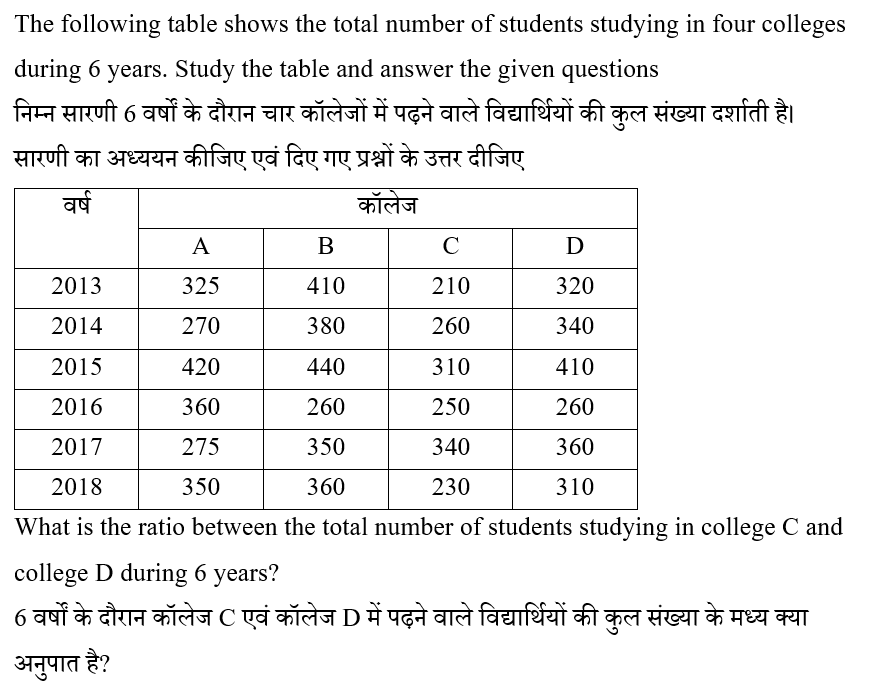
Question 7:
If the median of 5, 9, 11, x–3, 25, 27 and 32 is 19, then x = ?
यदि 5, 9, 11, x–3, 25, 27 एवं 32 की माध्यिका 19 हो, तो x = ?
Question 8:
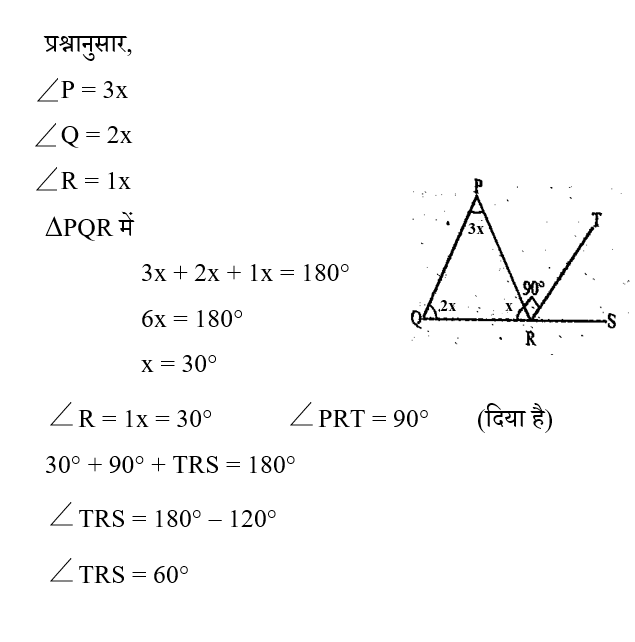
The side QR of a triangle PQR is produced to a point S and a line RT perpendicular to the side PR is drawn such that it is an acute angle. If ∠P : ∠Q : ∠R = 3 : 2 : 1, then the value of ∠TRS is :
त्रिभुज PQR की भुजा QR को एक बिंदु S तक बढ़ाया जाता है तथा भुजा PR पर लंब एक किरण RT इस प्रकार खींची जाती है कि एक न्यून कोण हो । यदि ∠P : ∠Q : ∠R = 3 : 2 : 1 है, तो ∠TRS का मान है-
Question 9:
The difference between the LCM and HCF of the numbers 450, 825 and 675 is:
संख्या 450, 825 और 675 के LCM और HCF का अंतर है -
Question 10:
In a class of 100 students, 1/4 of the total students like to play only football, 2/5 of the total students like to play only volleyball, and the remaining students like to play both the games. What fraction of the total students like to play both the games?
100 छात्रों की एक कक्षा में कुल छात्रों का 1/4 छात्र केवल फुटबॉल खेलना पसंद करते हैं, कुल छात्रों के 2/5 छात्र केवल वॉलीबॉल खेलना पसंद करते हैं, और शेष छात्र दोनों खेल खेलना पसंद करते हैं। कुल छात्रों का कितना भाग दोनों खेल खेलना पसंद करते हैं?